Can Elections Be Fair?

Imagine the United States had only three states, Texas, California and Florida. Suppose each of these states sent 10 delegates to the electoral college. Suppose, also, that each of these states is a swing state – the polls show 50% support for either candidate, so the result depends on tiny swings within each state.

Some years, Texas will be Republican, other years it will go to the Democrats. Same for the other two states. Any voter in any of the states could determine the outcome of the election. It seems all very fair (unless, of course, one state votes 99% for one party, while the other two vote 51% for the other). It’s fair to say that the elected President will try to keep the interests of the whole country at heart (or at least appear to), to avoid alienating anyone.

Imagine, though, that two of the states, California and Texas, decide to change matters – their ten counties will send a delegate who can vote independently of the other county delegates. (Currently, only two out of the 50 real states do something like this, and they’re both small.) Florida, however, continues to send 10 delegates who will all vote as a bloc.

Now comes the election. Suppose Florida goes to the Democrats by tiny margin. Already, the Democrat candidate has 10 delegates, and the Republican needs to win 15 or 16 of the remaining 20 in order to win. The chance of that, since each county chooses independently now, is less than one in 17. If instead the Republicans had taken Florida, they’d have a 16 in 17 chance of also taking the Presidency.

Only once in every 7 decades will Californian or Texan voters get a proper say in who their President is. Naturally, then, Presidents will focus on issues affecting Floridans instead of the whole country. At least, that is, until California and Texas repeal the change they made to their voting rules, or Florida follows their lead.

Of course, this is a simplified version of how the United States selects their President. However, it shows that big states voting as a bloc have power over smaller states. The best thing some swing states could do for themselves might be to merge with other states – at least electorally – to form factions of their own. Dakota, maybe? or Carolina? Fairer still would be to force each state’s delegates to vote for the President county by county, or voter by voter.

But would even that be fair? A now-famous theorem called Arrow’s Impossibility Theorem gives an amazing answer.

Imagine there was a candidate for President (call them Z) that, literally, nobody in the whole country liked. Everyone prefers either X or Y instead. In a fair system, they would come last. If they launched a massive PR campaign so that in 4 years time everyone liked them, they would – if the system was fair – come first. Somewhere along the line is a key voter, who switched from hating Z to loving them, moving Z off the bottom spot. The pivotal voter, if you will. Let’s call her Penny. Let’s imagine the campaign takes the form of a massively viral, completely persuasive Youtube video – which people watch one at a time, and as they watch it, their preferences change from “Z last” to “Z first”.

Where is Z just after Penny changes her mind? Let’s freeze the polls just there. Penny has just watched the famous video on Youtube – her attitude to Z changed, and Z moved out of last place. Let’s pause Z’s campaign for a moment.

Done.

Now, the key question – is Z coming second or first?

Ok, while Penny sits there, thinking about what she just saw,  X and Y ramp up their campaigns. First, X is wildly successful, so everyone prefers X. Then Y makes a stinging comeback and everyone prefers Y. They basically battle it out tooth and nail. How does this affect Z’s ranking?

Surely, in a fair system, whether Z beats Y should be determined by how much people prefer Z over Y, and not at all on who they prefer between Y and X. If Z is now beating Y, that won’t change, even if nobody likes X. That’s only possible if Z moved to the top of the list as Penny changed her vote.

So, as people change their preference for Z one by one, moving them from last to first, when the pivotal voter (Penny) makes this change, Z suddenly jumps from the underdog to the winner’s spot.

Well, not suddenly. Halfway through the video, she’s putting Z in between X and Y. Let’s suppose Penny likes X better than Y, so as she’s watching the video, Penny’s vote changes from X, Y, Z to X, Z, Y and finally to Z, X, Y. Everyone who’s already seen the video puts Z first, everyone who hasn’t still puts Z last.

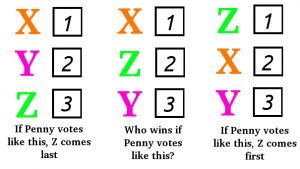
As Penny changes from X, Y, Z to X, Z, Y, it shouldn’t affect whether X beats Z, since everyone’s preferences between X and Z are still the same. When she put Z on the bottom, that was where Z ended up in the electoral result. Halfway through the video, Z is still below X. Likewise, in the second half of the video, Penny’s vote changes from X, Z, Y to Z, X, Y, making Z the winner. This change shouldn’t affect the result for Z vs Y.

So, the electoral preference of Y vs Z changes in the first half of the video (when Z escapes the bottom position) and the preference of X vs Z changes in the second half (when Z takes the lead). When Penny is halfway through the video, and is voting X above Z above Y, then as candidates, X is beating Z, who’s beating Y.

In other words, the election outcome is the same as Penny’s preferences. If Penny had preferred Y over Z over X halfway through the video, then Y would be beating X. In particular, Penny can choose whoever she likes between X and Y, and that determines which of them win, no matter which of them anyone else prefers. It’s one man one vote, and she’s the man who has the vote.

Penny has a lot of power.

And this power doesn’t actually depend on Z and her advertising campaign. After all, that campaign just changed preferences for Z viz other candidates. These shouldn’t affect whether or not X beats Y. So the result of X vs Y depends totally on Penny. We should just ask her, and save the trouble of having an election.

In fact, Penny has complete power over all the preferences. This same logic shows that there must be someone with complete power over the outcome between X and Z, and between Y and Z, but we’ve already seen that these preferences follow Penny’s as she watches the video.

This clearly can’t happen in a fair electoral system. This chain of logic shows that there is no such thing as

• a fair electoral system, where
• there’s more than 2 candidates, and
• people rank candidates in order of preference

 

In any such system, either

1. There’s a single voter who determines the outcome, OR
2. A change in preferences between some candidates might irrelevantly affect the outcome between some completely different candidates, OR
3. It’s possible for everyone to prefer a candidate and still have them lose.

 

This is Arrow’s Impossibility Theorem.

In most real electoral systems, it’s number 2 that gets violated. So it’s possible – possible – that right now, somewhere in Ohio or Florida or Nevada, there’s a voter tossing up between Gary Johnson and Jill Stein, not realizing that Barack Obama’s or Mitt Romney’s future hangs on their decision.